Задача #878 ← →
На полу лифта стоит теплоизолированный сосуд, открытый сверху. В сосуде под тяжёлым подвижным поршнем находится одноатомный идеальный газ. Изначально поршень находится в равновесии. Лифт начинает равноускоренно подниматься вверх.
-
Составьте уравнения, решениями которых будет зависимость координаты и температуры от времени. Известно, что адиабатический процесс описывается уравнением где коэффициент для одноатомного газа.
При расчетах, ежели таковые последуют, используйте следующие значения: масса поршня площадь сечения сосуда ускорение начальная высота поршня над дном сосуда количество вещества газа
-
Найдите конечную температуру если при движении на поршень действует сила трения
Решение
Примечание
-
Возможно, решение неверное. Есть сомнения.
-
Уравнение (7), по-видимому, не имеет аналитического решения в элементарных функциях. Решение получено численным интегрированием на
python, можно ознакомиться с кодом.Для физика главное — уметь правильно записать физические законы, а если аналитическое решение оказывается непосильным, на выручку приходят численные методы.
-
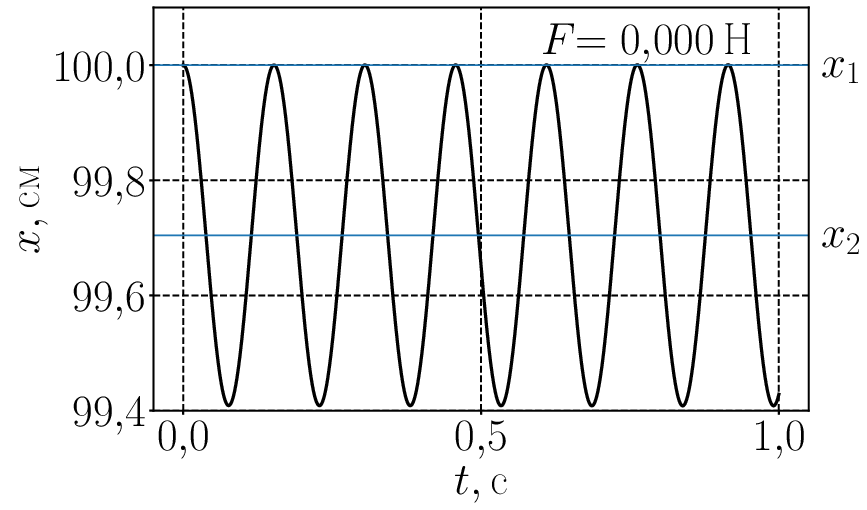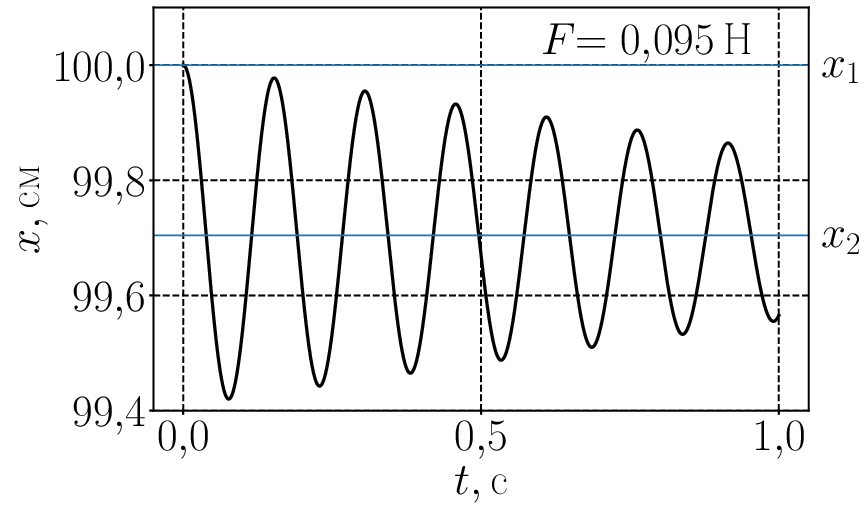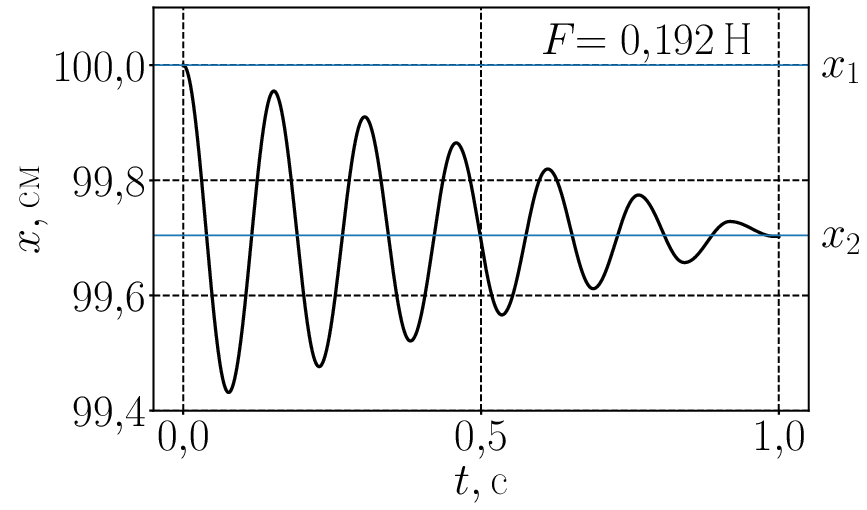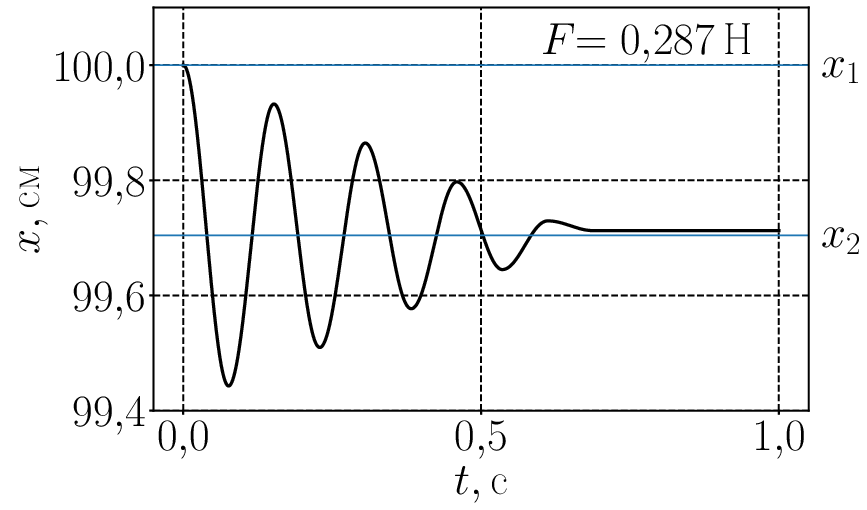
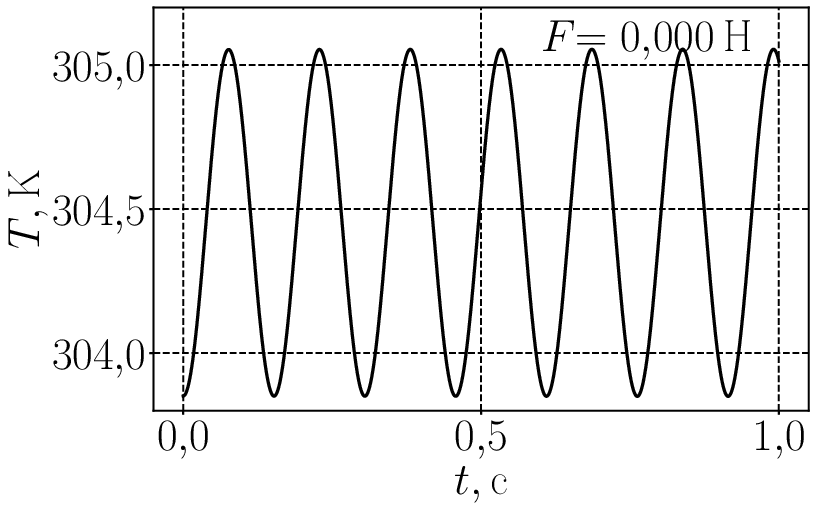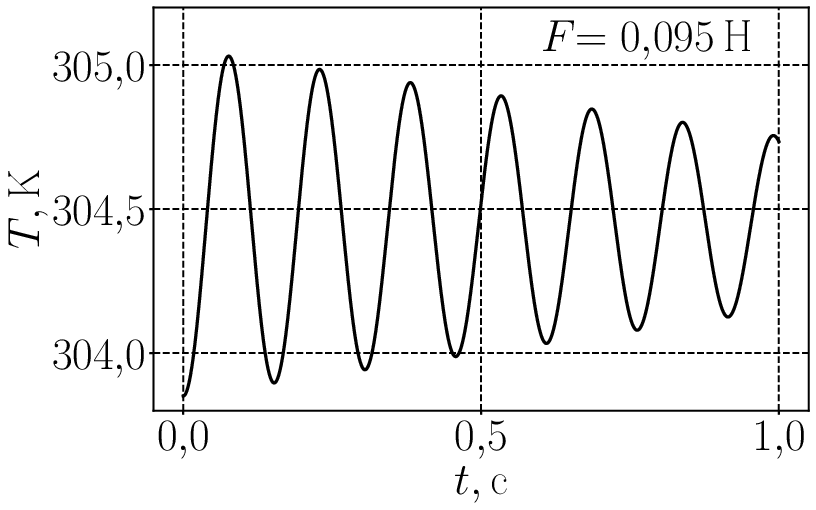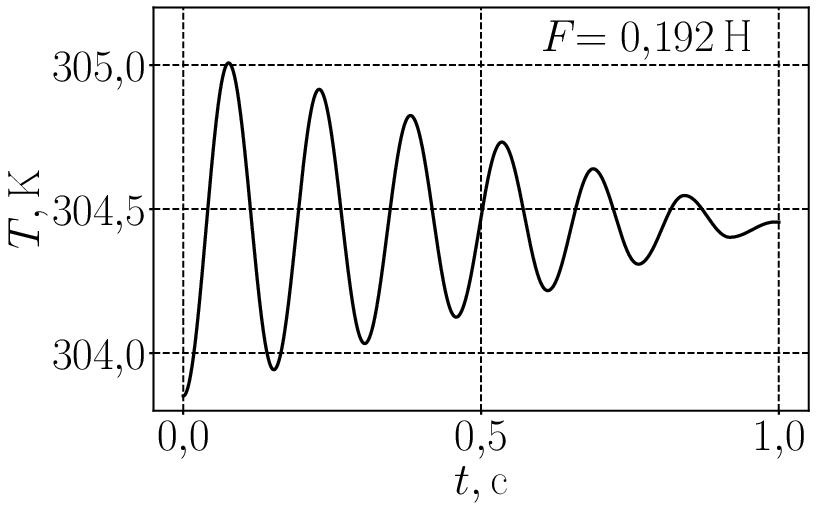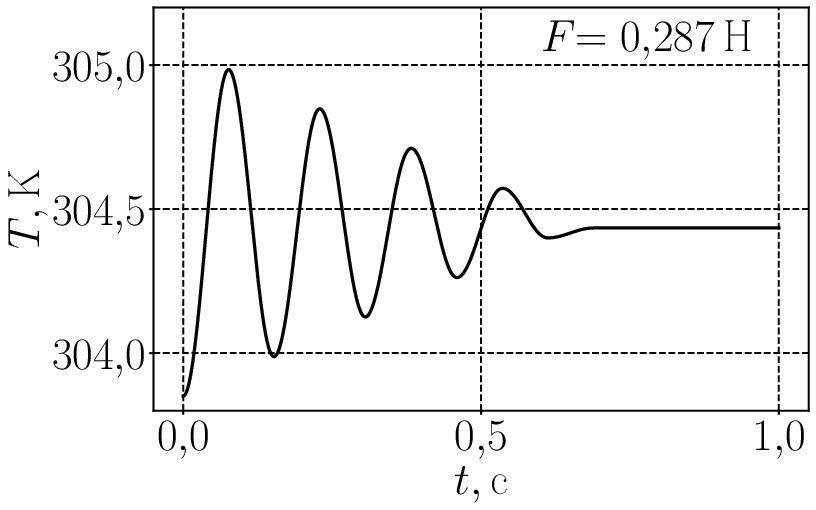
При включении сухого трения колебания не обязательно должны остановиться в положении равновесия которое определяется уравнением (2). Это хорошо видно на следующей анимации для где сила трения меняется от нуля до почти 0,3 Н. И следом анимированный график для температуры от времени Графики немного колбасит при силе трения поскольку код (по не вполне ясной для меня причине) испытывает в этой области некоторые затруднения.